svm算法伪代码（svm smo算法）

本篇文章给大家谈谈svm算法伪代码，以及svm smo算法对应的知识点，希望对各位有所帮助，不要忘了收藏本站喔。

本文目录一览：

• 1、SVM算法-推导
• 2、手撕SVM（公式推导+代码实现）（三）
• 3、如何利用 Python 实现 SVM 模型

SVM算法-推导

第一部分：从几何意义到数学表达

第三部分：SMO

求解第二部分最后推导出的最小化问题，每次固定两个lambda，由于有最后一个条件限制：lambdai*yi + lambdaj yj = const，labmdai可以用lambdaj表达出来，最小化函数是一个抛物线，开口朝上，求导，令导数为0，获得没有限制的最优化问题，由于lambdai = 0（第1个限制条件），做一个clipping，获得在限制条件下的lambdai最优解，然后也能求得lambdaj，就完成了一次lambdai和lambdaj的更新迭代。

一般取最违反KKT条件的lambdai和lambdaj来做更新。

svm软间隔

svm的核函数选择

一般选择高斯核函数，线性核函数是高斯核函数的一个特例；在特定的参数下，sigmoid核函数和高斯核函数具有类似的作用；相比于多项式核函数，高斯核函数的参数更少，更好调，当然，如果能把多项式核函数的参数调好，有可能会获得更好的效果。对于特征数量非常大的情况，会更倾向于使用线性核函数。

为什么要转化为对偶问题?

高斯核函数无限维的理解

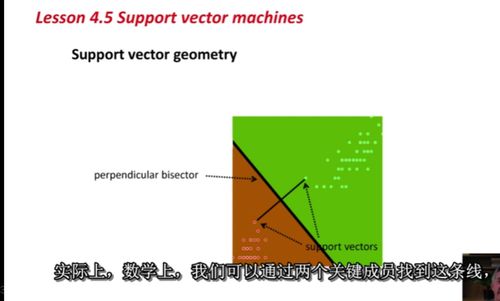
手撕SVM（公式推导+代码实现）（三）

前面我们进行了很多的理论性研究，下面我们开始用代码进行实现。

这个数据集显然线性可分。

[-1.0,

-1.0,

1.0,

-1.0,

1.0,

1.0,

1.0,

-1.0,

-1.0,

-1.0,

-1.0,

-1.0,

-1.0,

1.0,

-1.0,

1.0,

1.0,

-1.0,

1.0,

-1.0,

-1.0,

-1.0,

1.0,

-1.0,

-1.0,

1.0,

1.0,

-1.0,

-1.0,

-1.0,

-1.0,

1.0,

1.0,

1.0,

1.0,

-1.0,

1.0,

-1.0,

-1.0,

1.0,

-1.0,

-1.0,

-1.0,

-1.0,

1.0,

1.0,

1.0,

1.0,

1.0,

-1.0,

1.0,

1.0,

-1.0,

-1.0,

1.0,

1.0,

-1.0,

1.0,

-1.0,

-1.0,

-1.0,

-1.0,

1.0,

-1.0,

1.0,

-1.0,

-1.0,

1.0,

1.0,

1.0,

-1.0,

1.0,

1.0,

-1.0,

-1.0,

1.0,

-1.0,

1.0,

1.0,

1.0,

1.0,

1.0,

1.0,

1.0,

-1.0,

-1.0,

-1.0,

-1.0,

1.0,

-1.0,

1.0,

1.0,

1.0,

-1.0,

-1.0,

-1.0,

-1.0,

-1.0,

-1.0,

-1.0]

可以看出来，这里使用的类别标签是-1和1

SMO算法的伪代码：

L==H

第0次迭代 样本:1, alpha优化次数:1

第0次迭代 样本:3, alpha优化次数:2

第0次迭代 样本:5, alpha优化次数:3

L==H

第0次迭代 样本:8, alpha优化次数:4

L==H

j not moving enough

j not moving enough

L==H

L==H

j not moving enough

L==H

第0次迭代 样本:30, alpha优化次数:5

第0次迭代 样本:31, alpha优化次数:6

L==H

L==H

第0次迭代 样本:54, alpha优化次数:7

L==H

L==H

第0次迭代 样本:71, alpha优化次数:8

L==H

L==H

L==H

第0次迭代 样本:79, alpha优化次数:9

L==H

第0次迭代 样本:92, alpha优化次数:10

j not moving enough

L==H

迭代次数：0

第0次迭代 样本:1, alpha优化次数:1

j not moving enough

j not moving enough

j not moving enough

j not moving enough

j not moving enough

L==H

L==H

j not moving enough

j not moving enough

j not moving enough

j not moving enough

L==H

j not moving enough

L==H

L==H

j not moving enough

j not moving enough

第0次迭代 样本:37, alpha优化次数:2

第0次迭代 样本:39, alpha优化次数:3

第0次迭代 样本:52, alpha优化次数:4

j not moving enough

j not moving enough

j not moving enough

j not moving enough

j not moving enough

第0次迭代 样本:71, alpha优化次数:5

j not moving enough

j not moving enough

j not moving enough

j not moving enough

j not moving enough

迭代次数：0

j not moving enough

j not moving enough

j not moving enough

第0次迭代 样本:8, alpha优化次数:1

L==H

j not moving enough

第0次迭代 样本:23, alpha优化次数:2

L==H

j not moving enough

j not moving enough

L==H

j not moving enough

j not moving enough

j not moving enough

第0次迭代 样本:39, alpha优化次数:3

L==H

j not moving enough

第0次迭代 样本:52, alpha优化次数:4

j not moving enough

第0次迭代 样本:55, alpha优化次数:5

L==H

L==H

L==H

L==H

L==H

j not moving enough

第0次迭代 样本:79, alpha优化次数:6

第0次迭代 样本:92, alpha优化次数:7

迭代次数：0

j not moving enough

L==H

j not moving enough

j not moving enough

L==H

j not moving enough

第0次迭代 样本:23, alpha优化次数:1

j not moving enough

j not moving enough

j not moving enough

j not moving enough

j not moving enough

j not moving enough

j not moving enough

L==H

L==H

第0次迭代 样本:51, alpha优化次数:2

j not moving enough

j not moving enough

j not moving enough

j not moving enough

L==H

第0次迭代 样本:69, alpha优化次数:3

L==H

j not moving enough

第0次迭代 样本:94, alpha优化次数:4

j not moving enough

j not moving enough

迭代次数：0

j not moving enough

j not moving enough

j not moving enough

j not moving enough

j not moving enough

...

迭代次数：497

j not moving enough

j not moving enough

j not moving enough

迭代次数：498

j not moving enough

j not moving enough

j not moving enough

迭代次数：499

j not moving enough

j not moving enough

j not moving enough

迭代次数：500

如何利用 Python 实现 SVM 模型

我先直观地阐述我对SVM的理解，这其中不会涉及数学公式，然后给出Python代码。

SVM是一种二分类模型，处理的数据可以分为三类：

线性可分，通过硬间隔最大化，学习线性分类器

近似线性可分，通过软间隔最大化，学习线性分类器

线性不可分，通过核函数以及软间隔最大化，学习非线性分类器

线性分类器，在平面上对应直线；非线性分类器，在平面上对应曲线。

硬间隔对应于线性可分数据集，可以将所有样本正确分类，也正因为如此，受噪声样本影响很大，不推荐。

软间隔对应于通常情况下的数据集（近似线性可分或线性不可分），允许一些超平面附近的样本被错误分类，从而提升了泛化性能。

如下图：

实线是由硬间隔最大化得到的，预测能力显然不及由软间隔最大化得到的虚线。

对于线性不可分的数据集，如下图：

我们直观上觉得这时线性分类器，也就是直线，不能很好的分开红点和蓝点。

但是可以用一个介于红点与蓝点之间的类似圆的曲线将二者分开，如下图：

我们假设这个黄色的曲线就是圆，不妨设其方程为x^2+y^2=1，那么核函数是干什么的呢？

我们将x^2映射为X，y^2映射为Y，那么超平面变成了X+Y=1。

那么原空间的线性不可分问题，就变成了新空间的（近似）线性可分问题。

此时就可以运用处理（近似）线性可分问题的方法去解决线性不可分数据集的分类问题。

---------------------------------------------------------------------------------------------------------------------------

以上我用最简单的语言粗略地解释了SVM，没有用到任何数学知识。但是没有数学，就体会不到SVM的精髓。因此接下来我会用尽量简洁的语言叙述SVM的数学思想，如果没有看过SVM推导过程的朋友完全可以跳过下面这段。

对于求解（近似）线性可分问题：

由最大间隔法，得到凸二次规划问题，这类问题是有最优解的（理论上可以直接调用二次规划计算包，得出最优解）

我们得到以上凸优化问题的对偶问题，一是因为对偶问题更容易求解，二是引入核函数，推广到非线性问题。

求解对偶问题得到原始问题的解，进而确定分离超平面和分类决策函数。由于对偶问题里目标函数和分类决策函数只涉及实例与实例之间的内积，即xi,xj。我们引入核函数的概念。

拓展到求解线性不可分问题：

如之前的例子，对于线性不可分的数据集的任意两个实例：xi,xj。当我们取某个特定映射f之后，f(xi)与f(xj)在高维空间中线性可分，运用上述的求解（近似）线性可分问题的方法，我们看到目标函数和分类决策函数只涉及内积f(xi),f(xj)。由于高维空间中的内积计算非常复杂，我们可以引入核函数K(xi,xj)=f(xi),f(xj)，因此内积问题变成了求函数值问题。最有趣的是，我们根本不需要知道映射f。精彩！

我不准备在这里放推导过程，因为已经有很多非常好的学习资料，如果有兴趣，可以看：CS229 Lecture notes

最后就是SMO算法求解SVM问题，有兴趣的话直接看作者论文：Sequential Minimal Optimization:A Fast Algorithm for Training Support Vector Machines

我直接给出代码：SMO+SVM

在线性可分数据集上运行结果：

图中标出了支持向量这个非常完美，支持向量都在超平面附近。

在线性不可分数据集上运行结果（200个样本）：

核函数用了高斯核，取了不同的sigma

sigma=1，有189个支持向量，相当于用整个数据集进行分类。

sigma=10，有20个支持向量，边界曲线能较好的拟合数据集特点。

我们可以看到，当支持向量太少，可能会得到很差的决策边界。如果支持向量太多，就相当于每次都利用整个数据集进行分类，类似KNN。

svm算法伪代码的介绍就聊到这里吧，感谢你花时间阅读本站内容，更多关于svm smo算法、svm算法伪代码的信息别忘了在本站进行查找喔。